Question

Explain in words why each of the following integrals is improper. (a) integral from 2^(infinity) t^7 e^(-t^2) dt. (b) integral from (pi/4)^(pi/2) sec t dt. (c) integral from 1^3[dt]/[|t-2|] . (d) integral from 1^2 ln (t-1) dt.

Answer 1

1. Integral defined in an improper interval

`\int\limits^\infty_2 {t^7 e^(-t^2)} \, dt`

2. Integral of a function undefined at some point of the interval.

`\int\limits^(\pi/2)_ {\pi/4} {sec(t)}\, dt`

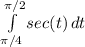
3. Integral of a function undefined at some point of the interval

`\int\limits^3_1 )`

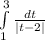
4. Integral of a function undefined at some point of the interval

`\int\limits_(1)^(2) {ln(t-1)} \, dt\\`

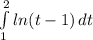
Explanation:

Remember that there two types of undefined integrals.

1 - Integrals that are computer over an unbounded interval (in other words one of the limits is infinity )

2 - Integrals where the function is undefined at some point of the interval.

So, identify the first type the first type of improper integrals a kind of straightforward, but for the second type of improper integrals you need to understand the function you are integrating.

By "undefined" it is understood that the function has some kind of discontinuity, for example, the function

`f(x) = 1/x`

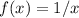
is discontinuous at 0.

Now lets see the examples given.

`Sec(t) = 1/cos(t)`

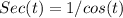
Rememebr that
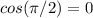`cos(\pi/2) = 0` , that's why the function the second integral is improper.

For the next function

`f(t) = (1)/(|t-2|)`

`f(2) = (1)/(|2-2|) = 1/0`

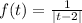
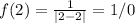
Thats a discontinuity as well, and 2 belongs to the interval of integration, that's why that integral would be improper.

And for the next one, remember that the
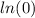`ln(0)` is not defined, therefore,

`f(t) = ln(t-1)\\f(1)=ln(1-1)=ln(0)`

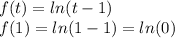
and 1 , belongs to the interval of integration, that's why it would be an improper integral.