Question

A retail outlet for calculators sells 900 calculators per year. It costs ​$2 to store one calculator for a year. To​ reorder, there is a fixed cost of ​$4​, plus ​$1.25 for each calculator. How many times per year should the store order​ calculators, and in what lot​ size, in order to minimize inventory​ costs?

Answer 1

In order to minimize cost the outlet must order 60 units 15 times a year.

Step-by-step explanation:

Theoretically, the EOQ is the optimal order quantity that a firm should purchase in order to minimize its inventory costs (holding costs are included here), and costs of placing an order.

Mathematically:

EOQ=
`√(2SD) /H`

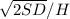
Where:

D= demand

S= cost of placing an order.

H= holding cost (per unit and per year).

In the statement, we identify each of these values:

D= 900

S= 4

H= $2

EOQ=
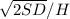`√(2SD) /H`=√2*4*900/2= 60

Times per year= 900/60= 15