Question

4. Two particles, A and B, are in uniform circular motion about a common center. The acceleration of particle A is 7.3 times that of particle B. The period of particle B is 2.5 times the period of particle A. The ratio of the radius of the motion of particle A to that of particle B is closest to

Answer 1

The ratio of he radius of the motion of particle A to that of particle B is closest to 1.16.

Step-by-step explanation:

Let
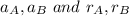`a_A,a_B\ and\ r_A,r_B` are accelerations of particle and radius of A and B respectively. It is given that :

`a_A=7.3* a_B\\\\(a_A)/(a_B)=7.3\\\\and\\\\T_B=2.5* T_A\\(T_B)/(T_A)=2.5`

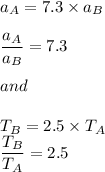
The centripetal acceleration is given by the formula as :

`a=(v^2)/(r)`

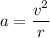
r is the radius of motion

Since,
`v=(2\pi r)/(T)`

`a=(4\pi ^2r)/(T^2)`

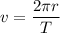
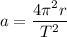
For A

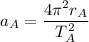`a_A=(4\pi^2 r_A)/(T^2_A)`.........(1)

For B

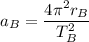`a_B=(4\pi^2 r_B)/(T^2_B)`...........(2)

Dividing equation (1) and (2) we get :

`(a_A)/(a_B)=(T^2_B* r_A)/(T^2_A* r_B)`

`(r_A)/(r_B)=(a_A* T^2_A)/(a_B* T^2_B)`

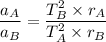
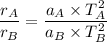
Now using given conditions :

`(r_A)/(r_B)=(7.3)/((2.5)^2)\\\\(r_A)/(r_B)=1.16`

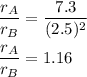
So, the ratio of he radius of the motion of particle A to that of particle B is closest to 1.16.

Answer 2

Step-by-step explanation:

Acceleration of particle A is 7.3 times the acceleration of particle B.

Let the acceleration of particle B is a, then the acceleration of particle A is

7.3 a.

Let the period of particle A is T and the period of particle B is 2.5 T.

Let the radius of particle A is RA and the radius of particle B is RB.

Use the formula for the centripetal force

`a=r\omega ^(2)=r* (4\pi^(2))/(T^(2))`

So,
`r = a(T^(2))/(4\pi^(2))`

The ratio of radius of A to the radius of B is given by

`(R_(A))/(R_(B))=(a_(A)* T_(A)^(2))/(a_(B)* T_(B)^(2))`

`(R_(A))/(R_(B))=(7.3 a* T^(2))/(a* 6.25T^(2))`

RA : RB = 1.17