Question

An owner of a key rings manufacturing company found that the profit earned (in thousands of dollars) per day by selling n number of key rings is given by , where n is the number of key rings in thousands. Find the number of key rings sold on a particular day when the total profit is $5,000.

Answer 1

The number of key rings sold on a particular day when the total profit is $5,000 is 4,000 rings.

Explanation:

The question is incomplete.

An owner of a key rings manufacturing company found that the profit earned (in thousands of dollars) per day by selling n number of key rings is given by

`P=n^2-2n-3`

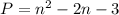
where n is the number of key rings in thousands.

Find the number of key rings sold on a particular day when the total profit is $5,000.

We have the profit defined by a quadratic function.

We have to calculate n, for which the profit is $5,000.

`P=n^2-2n-3=5\\\\n^2-2n-8=0`

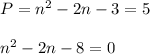
We have to calculate the roots of the polynomial we use the quadratic equation:

`n=(-b\pm√(b^2-4ac))/(2a)\\\\n= (-2\pm√(4-4*1*(-8)))/(2)= (-2\pm√(4-32))/(2) = (-2\pm√(36))/(2) =(-2\pm6)/(2) \\\\n_1=(-2-6)/2=-8/2=-4\\\\n_2=(-2+6)/2=4/2=2`

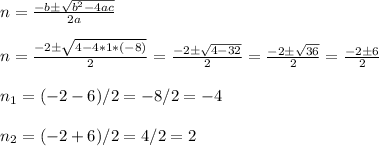
n1 is not valid, as the amount of rings sold can not be negative.

Then, the solution is n=4 or 4,000 rings sold.