Answer:
100 times
Step-by-step explanation:
The sound intensity level β of a sound with an intensity I is mathematically given as:
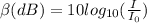 , Where
, Where
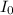 = lowest sound intensity for a normal person at a frequency of 1000 Hz
= lowest sound intensity for a normal person at a frequency of 1000 Hz
For the quiet part:
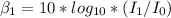
For the loud part:
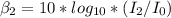
Hence,
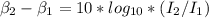
70-50 =
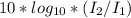
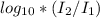 = 2
= 2
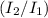 = 100
= 100
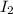 = 100
= 100
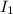
Therefore, the latter sound (
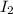 ) is 100 times louder than the former sound (
) is 100 times louder than the former sound (
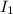 )
)