Question

In a double-slit interference pattern the path length from one slit to the first bright fringe of a double-slit interference pattern is longer than the path length from the other slit to the fringe by:A.one-quarter of a wavelength.B.one-half of a wavelength.C.one full wavelength.D.three-quarters of a wavelength.E.two full wavelengths

Answer 1

C.one full wavelength.

Step-by-step explanation:

In a double-slit experiment, the figure projected on the distant screen shows alternating bright fringes (constructive interference) and dark fringes (destructive interference).

The conditions for the two types of interference are the following:

- Constructive interference (bright fringe) occurs when the path length difference between the two slits is an integer multiple of the wavelength, so when

`|d_1 -d_2|=n\lambda`

where
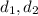`d_1,d_2` are the path length from the two slits, n is an integer, and
`\lambda` is the wavelength.

- Destructive interference (dark fringe) occurs when the path length difference between the two slits is an odd multiple of half-wavelength, so when

`|d_1 -d_2|=(n+(1)/(2))\lambda`

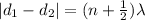
where n is an integer.

Here we want to know what happens at the first bright fringe (next to the central bright fringe). Since it is a bright fringe, the path difference must be an integer multiple of the wavelength. Moreover, the central maximum is the one having

n = 0

Therefore, the first bright fringe next to it will be the one having

n = 1

This means that the correct answer is

C.one full wavelength.