Question

A radio station runs a promotion at an auto show with a money box with 15 ​$50 ​tickets, 11 ​$25 ​tickets, and 15 ​$5 tickets. The box contains an additional 20 ​"dummy" tickets with no value. Three tickets are randomly drawn. Find the probability that all three tickets have no value.

Answer 1

0.0316

Explanation:

Given:

A radio station runs a promotion at an auto show with a money box with 15 ​$50 ​tickets, 11 ​$25 ​tickets, and 15 ​$5 tickets.

The box contains an additional 20 ​"dummy" tickets with no value.

Thus, total number of tickets = 15 + 11 + 15 + 20 = 61

Three tickets are randomly drawn.

Question asked:

Find the probability that all three tickets have no value.

Solution

As we know:

`Probability =(Favourable \ outcome)/(Total\ outcome)`

First of all we will find favorable outcome for drawing 3 dummy tickets.

Favorable outcome for drawing 3 dummy tickets out of 15 $50 ​tickets =
`^(15) C_(0)`

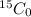
Favorable outcome for drawing 3 dummy tickets out of 11 $25 ​tickets =
`^(11) C_(0)`

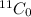
Favorable outcome for drawing 3 dummy tickets out of 15 $5 ​tickets =
`^(15) C_(0)`

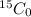
Favorable outcome for drawing 3 dummy tickets out of 20 dummy ticket =
`^(20) C_(3)`

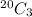
Thus, total Favorable outcome for drawing 3 dummy tickets =

`^(15) C_(0)*^(11) C_(0)*^(15) C_(0)*^(20) C_(3)`

`(15!)/((15-0)!0!) *(11!)/((11-0)!0!) *(15!)/((15-0)!0!) *(20!)/((20-3)!3!)`

`(15!)/(15!*1) *(11!)/(11!*1) *(15!)/(15!*1) *(20*19*18*17!)/(17!\imes3*2*1) \\\\ 1*1*1*(6840)/(6) \\\\ =1140`

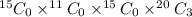
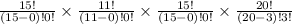
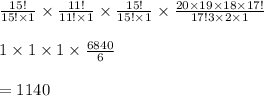
Total outcome for drawing 3 dummy tickets out of 61 tickets =
`^(61) C_(3)=(61!)/((61-3)!*3) =(61*60*59*58!)/(58!*3*2*)=(215940)/(6) =35990`

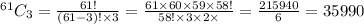
Now,

`Probability =(Favourable \ outcome)/(Total\ outcome)\\`

`=(1140)/(35990) =0.0316\\`

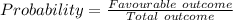
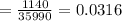
Thus, the probability of three tickets that are randomly drawn are dummy tickets is 0.0316