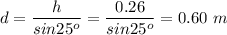Question

An ice cube of mass 50.0 gg can slide without friction up and down a 25.0 degreedegree slope. The ice cube is pressed against a spring at the bottom of the slope, compressing the spring 0.100 mm . The spring constant is 25.0 N/mN/m . When the ice cube is released, how far will it travel up the slope before reversing direction

Answer 1

We have assumed the distance to be 0.1 meters (not millimeters) since the question has issues when expressing the units

Answer:

`d=0.60\ m`

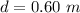
Step-by-step explanation:

Energy Conversion

We need to understand and apply the concepts of energy conversion to solve this problem. Three types of energy are manifested in the motion of the ice cube of mass m.

When it's above the ground level at a height h, it has potential gravitational energy, given by

`U=mgh`

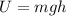
If the cube is moving at speed v, it has kinetic energy, given by

`\displaystyle K=(1)/(2)mv^2`

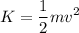
Finally, when it compresses the spring, it has elastic energy:

`\displaystyle E=(1)/(2)kx^2`

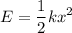
Where x is the distance of compression and k is the spring constant

When the ice cube is released, it has potential gravitational energy which magnitude we cannot calculate since we don't have the height. Then it goes down the slope and acquires speed and kinetic energy until it stops when compressing the spring a distance x. In that very moment, the total energy is stored in its elastic form:

`\displaystyle E=(1)/(2)25\cdot 0.1^2=0.125\ J`

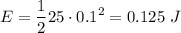
When the ice cube travels up powered by that energy, it has both kinetic and potential energies, and it stops up in the ramp and starts reversing direction when it runs out of speed, thus the total potential energy is

`mgh=0.125\ J`

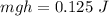
Solving for h, knowing m=50 g=0.05 Kg

`\displaystyle h=(0.125)/(mg)=(0.125)/(0.05\cdot 9.8)=0.26\ m`

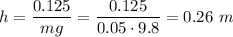
The height and the distance traveled in the slope d are related by

`h=d.sin25^o`

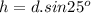
Thus

`\displaystyle d=(h)/(sin25^o)=(0.26)/(sin25^o)=0.60\ m`

`\boxed {d=0.60\ m}`