Question

A trough is filled with a liquid of density 875 kg/m3. The ends of the trough are equilateral triangles with sides 6 m long and vertex at the bottom. Find the hydrostatic force on one end of the trough. (Use 9.8 m/s2 for the acceleration due to gravity.)

Answer 1

The hydrostatic force on one end of a trough with equilateral triangular ends and a liquid of density 875 kg/m³ can be calculated using the integral of hydrostatic pressure over the area, considering the triangular shape's geometry and fluid density.

Step-by-step explanation:

Calculating Hydrostatic Force on a Trough

The student's question is regarding the calculation of the hydrostatic force exerted on one end of a trough, where the ends are shaped as equilateral triangles and the liquid within the trough has a given density. To calculate this force, we will use principles of fluid pressure and static fluids.

First, we calculate the area of the triangular end, using the formula for the area of an equilateral triangle, which is A = (\(\√{3}/4))\(s²), where s is the side of the triangle. Thus, A = (\(\√{3}/4))(6 m)² = 15.59 m².

The hydrostatic pressure at any depth y in a fluid is given by p =
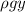`\(\rho g y`, where
`\(\rho` is the density of the liquid, g is the acceleration due to gravity, and y is the depth. Since pressure varies with depth, we must integrate over the entire surface to find the total force. The total force is the integral of pressure over the area which, due to symmetry, can be calculated as F =
`\(\int_(0)^(h) \rho g y dy`, with h being the height of the triangle.

For an equilateral triangle with side 6 m, the height h is \(h = (\√{3}/2)s =
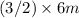`(\√{3}/2)* 6 m` = 5.20 m.

Integrating the hydrostatic pressure over the height of the triangle, we get F =
`\(\rho g (h²)/(2) * A`. Plugging in the values we have
`\(\rho` = 875 kg/m³), g = 9.8 m/s², h = 5.20 m, and A = 15.59 m².
Plugging in the values, we have A = (√3/4) × (6 m)² = 9√3 m². Now we can calculate the force:

F = (875 kg/m³)(9.8 m/s²)(6 m)(9√3 m²) ≈ 230948.99 N

Answer 2

The force on one end of the trough is 5.4 X 10⁵ N

Step-by-step explanation:

The triangle is equilateral which means all the interior angles are 60° and the sides are 6m long.

According to the figure,

AI / 8 = sin (60) = √3/2

AI = 4√3

The depth of the water is AI = 4√3

The interval becomes, | 0 , 4√3|

w = 2JK

`w = (2)/(√(3) ) (4√(3) - y')\\\\P_i = pgy\\\\F_i = pgy' X (2)/(√(3) ) (4√(3) - y')dy` (the hydrostatic force acting on the strip is the product of the pressure and the area)

where.

ρ = 875 kg/m³

g = 9.8m/s²

d = depth ( d = y')

`\lim_(n \to \infty) E^n_1 F_i\\\\ \lim_(n \to \infty) E^n_1 pgy' (2)/(√(3) ) (4√(3) - y')dy\\\\= \int\limits^4_0 {pgy (2)/(√(3) )(4√(3) - y) } \, dy\\\\= (2pg)/(√(3) ) \int\limits^4_0 {4√(3) - y) } \, dy`

limit is 0 → 4√3

On solving the equation, we get the value of limit as 32√3

`F = (2pg)/(√(3) ) X 32√(3) = 64pg\\\\F = 64 X 875 X 9.8\\\\F = 548800N`

Therefore, the force on one end of the trough is 5.4 X 10⁵ N