Question

Margin of error and the confidence interval. A study of stress on the campus of your university reported a mean stress level of 78 (on a 0 to 100 scale with a higher score indicating more stress) with a margin of error of 5 for 95% confidence. The study was based on a random sample of 64 undergraduates. (a) Give the 95% confidence interval. (b) If you wanted 99% confidence for the same study, would your margin of error be greater than, equal to, or less than 5

Answer 1

(a) The 95% confidence interval for the population mean stress level is (73, 83).

(b) Increasing the confidence level to 99% from 95% the margin of error would be greater than 5.

Explanation:

The (1 - α) % confidence interval for population mean is:

`CI=\bar x\pm MOE`

The information provided is:

`\bar x` = 78

Confidence level = 95%

MOE = 5

(a)

Compute the 95% confidence interval for the population mean stress level as follows:

`CI=\bar x\pm MOE\\=78\pm5\\=(73, 83)`

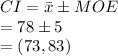
Thus, the 95% confidence interval for the population mean stress level is (73, 83).

(b)

The formula to compute the margin of error (MOE) is:

`MOE=z_(\alpha/2)(\sigma)/(√(n))`

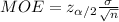
The margin of error is affected by:

1. Standard deviation
2. Sample size
3. Confidence level.

On increasing the confidence level the critical value of z increases.

`z_(90\%)=1.645\\z_(95\%)=1.96\\z_(99\%)=2.58`

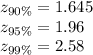
And if the critical value is increased then the margin of error will also increase.

Thus, increasing the confidence level to 99% from 95% the margin of error would be greater than 5.