Question

Xavier and Yolanda both have classes that end at noon and they agree to meet every day after class. They arrive at the coffee shop independently. Xavier's arrival time is X and Yolanda's arrival time is Y, where X and Y are measured in minutes after noon. The individual density functions are given. (Xavier arrives sometime after noon and is more likely to arrive promptly than late. Yolanda always arrives by 12:10 PM and is more likely to arrive late than promptly.) After Yolanda arrives, she'll wait for up to 45 minutes for Xavier, but he won't wait for her. Find the probability that they meet. (Round your answer to three decimal places.)

Answer 1

`\mathbf{ \int_(0)^(10) \int_(y)^(y+45) f(x)g(y)dxdy }`

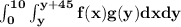
Explanation:

Ask yourself, when will Xavier and Yolanda meet??

Firstly, since it is given that Xavier doesn't wait at all, in order for them to meet, Yolanda must arrive before Xavier. This in mathematical terms can be expressed as

`Y \leq X`

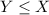
Secondly, Yolanda will wait for only 45 minutes, So Xavier must arrive before that, i.e

`X \leq Y+45`

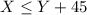
Combining both conditions, we obtain

`Y \leq X \leq Y+45`

If
`f(x)` and
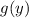`g(y)` be the density functions for Xavier and Yolanda respectively, the probability of meeting is given by,

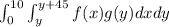`\int_(0)^(10) \int_(y)^(y+45) f(x)g(y)dxdy`.