Answer:
Therefore,
∠A = 30°
∠B = 60°
∠C = 150°
∠D = 120°
Explanation:
Given:
A puzzle in the form of a quadrilateral is inscribed in a circle.
The vertices A ,B ,C ,D of the quadrilateral divide the circle into four arcs in a ratio of 1 : 2 : 5 : 4.
Let the common multiple be "x" then the angles will be
∠A = 1x
∠B = 2x
∠C = 5x
∠D = 4x
To Find:
The angle measures of the quadrilateral = ?
Solution:
In a Quadrilateral inscribed in a Circle,
Sum of the measure of all the angles in a Quadrilateral is 360°
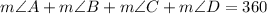
Substituting the values we get
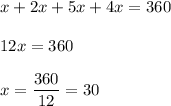
Therefore the measures are
∠A = 30°
∠B = 2 × 30 = 60°
∠C = 5 × 30 = 150°
∠D = 4 × 30 = 120°
Therefore,
∠A = 30°
∠B = 60°
∠C = 150°
∠D = 120°