Question

A parking space shaped like a parallelogram has a base of 18 feet and a height is 9 feet. A car parked in the space is 13 feet long and 5 feet wide. How much of the parking space is not covered by the car?

Answer 1

Explanation:

Given:

Parallelogram:

Height, h = 9 ft

Base, b = 18 ft

Rectangle:

Length, l = 13 ft

Width, b = 5 ft

Area of a parallelogram (parking space) = b × h

= 18 × 9

= 162 ft^2

Area of a rectangle (car) = b × l

= 13 × 5

= 65 ft^2

Area not covered by the car = area of the parking space - area of the car

= 162 - 65

= 97 ft^2

% of the parking space = area not covered/area of the parking space × 100

= 97/162 × 100

= 59.88 %

Answer 2

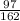`(97)/(162)` or 59.88% of the parking space is not covered by the car.

Explanation:

This question deals with the area of a space.

We need to find the area covered by the car, and compare with the area of the parking space.

The area of the car (which we will assume in this case, is more like a rectangle) = Length × Breadth = 13 feet × 5 feet = 65 fee
`t^(2)`

The area of the parking space (a parallelogram) is base × height = 18 feet × 9 feet = 162 fee
`t^(2)`

The amount of the parking space occupied by the car is then given by
`(Area Of Car)/(Area Of Parking Space)` =
`(65 feet^2)/(162 feet^2)` =
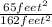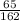`(65)/(162)` or 40.12%

So, the area not covered by the car is gotten by subtracting the area covered by the car (which is a fraction), from 1.

So, 1 -
`(65)/(162)` =
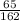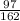`(97)/(162)` or 59.88% of the parking space