Question

What is the coefficient of x2y3 in the expansion of (2x + y)5?

ОА. 2
Ов. 5
Ос. 40
OD.
E. It does not exist.

Answer 1

Option C:

The coefficient of
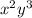`x^(2) y^(3)` is 40.

Solution:

Given expression:

`(2 x+y)^(5)`

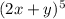
Using binomial theorem:

`(a+b)^(n)=\sum_(i=0)^(n)\left(\begin{array}{l}n \\i\end{array}\right) a^((n-i)) b^(i)`

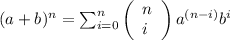
Here
`a=2 x, b=y`

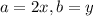
Substitute in the binomial formula, we get

`(2x+y)^5=\sum_(i=0)^(5)\left(\begin{array}{l}5 \\i\end{array}\right)(2 x)^((5-i)) y^(i)`

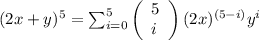
Now to expand the summation, substitute i = 0, 1, 2, 3, 4 and 5.

`$=(5 !)/(0 !(5-0) !)(2 x)^(5) y^(0)+(5 !)/(1 !(5-1) !)(2 x)^(4) y^(1)+(5 !)/(2 !(5-2) !)(2 x)^(3) y^(2)+(5 !)/(3 !(5-3) !)(2 x)^(2) y^(3)`

`$+(5 !)/(4 !(5-4) !)(2 x)^(1) y^(4)+(5 !)/(5 !(5-5) !)(2 x)^(0) y^(5)`

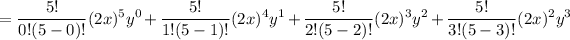
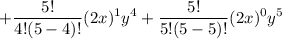
Let us solve the term one by one.

`$(5 !)/(0 !(5-0) !)(2 x)^(5) y^(0)=32 x^(5)`

`$(5 !)/(1 !(5-1) !)(2 x)^(4) y^(1) = 80 x^(4) y`

`$(5 !)/(2 !(5-2) !)(2 x)^(3) y^(2)= 80 x^(3) y^(2)`

`$(5 !)/(3 !(5-3) !)(2 x)^(2) y^(3)= 40 x^(2) y^(3)`

`$(5 !)/(4 !(5-4) !)(2 x)^(1) y^(4)= 10 x y^(4)`

`$(5 !)/(5 !(5-5) !)(2 x)^(0) y^(5)=y^(5)`

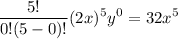
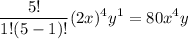
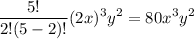
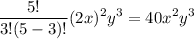
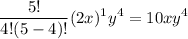
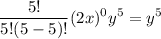
Substitute these into the above expansion.

`(2x+y)^5=32 x^(5)+80 x^(4) y+80 x^(3) y^(2)+40 x^(2) y^(3)+10 x y^(4)+y^(5)`

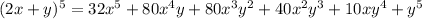
The coefficient of
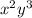`x^(2) y^(3)` is 40.

Option C is the correct answer.