Answer:
L= 2 mH
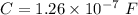
Step-by-step explanation:
Given that
Frequency , f= 10 kHz
Maximum current ,I = 0.1 A
Maximum energy stored ,E= 1 x 10⁻⁵ J
The maximum energy stored in the inductor is given as follows
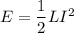
Where ,L= Inductance
I=Current
E=Energy
Now by putting the values in the above equation
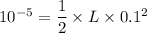
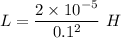
L=0.002 H
L= 2 mH
We know that frequency f is given as
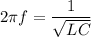
C=Capacitance , f=frequency ,L=Inductance
Now by putting the values
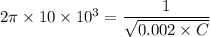
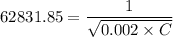
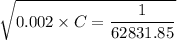
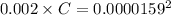
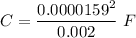
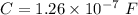
Therefore the inductance and capacitance will be 2 mH and 1.26 x 10⁻⁷ F respectively.