Question

#4 Find x. Assume that segments that appear tangent are tangent. *

Answer 1

The value of x is 7

Step-by-step explanation:

Given that the length of HN = 11 and HK = 18

We need to determine the value of x.

Length of HJ:

The circle theorem states that "two tangents from an external point to the circle are always equal in length".

Thus, from the figure, the tangents HN and HJ are tangents from an external point H will have the same length.

Thus, we have,

`HN = 11 = HJ`

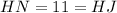
Thus, the length of HJ is 11

Length of JK:

The length of JK can be determined by subtracting the length of HK and HJ.

Thus, we have,

`JK=HK-HJ`

`JK=18-11`

`JK=7`

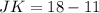
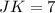
Thus, the length of JK is 7

Length of x:

Using the circle theorem, JK and KL are the tangents from an external point K, then the two tangents will have the same length.

Thus, we have,

`JK=7=KL`

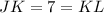
Hence, KL = x = 7

Thus, the value of x is 7