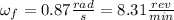Question

A playground merry-go-round of radius R = 2.20 m has a moment of inertia I = 260 kg · m2 and is rotating at 12.0 rev/min about a frictionless vertical axle. Facing the axle, a 24.0-kg child hops onto the merry-go-round and manages to sit down on the edge. What is the new angular speed of the merry-go-round?

Answer 1

The new angular speed of the merry-go-round is 8.31 rev/min.

Step-by-step explanation:

Because the merry-go-round is rotating about a frictionless axis there’re not external torques if we consider the system merry-go-round and child. Due that we can apply conservation fo angular momentum that states initial angular momentum (Li) should be equal final angular momentum (Lf):

`L_f=L_i` (1)

The initial angular momentum is just the angular momentum of the merry-go-round (Lmi) that because it's a rigid body is defined as:

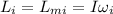`L_i=L_(mi)=I\omega_i` (2)

with I the moment of inertia and ωi the initial angular speed of the merry-go-round

The final angular momentum is the sum of the final angular momentum of the merry-go-round plus the final angular momentum of the child (Lcf):

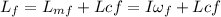`L_f=L_(mf)+L{cf}=I\omega_f+L{cf}` (3)

The angular momentum of the child should be modeled as the angular momentum of a punctual particle moving around an axis of rotation, this is:

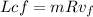`L{cf}=mRv_f` (4)

with m the mass of the child, R the distance from the axis of rotation and vf is final tangential speed, tangential speed is:

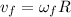`v_f=\omega_f R` (5)

(note that the angular speed is the same as the merry-go-round)

using (5) on (4), and (4) on (3):

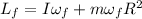`L_f=I\omega_f+m\omega_f R^2` (6)

By (5) and (2) on (1):

`I\omega_f+m\omega_f R^2=I\omega_i`

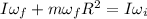
Solving for ωf (12.0 rev/min = 1.26 rad/s):

`\omega_f= (I\omega_i)/(]I+mR^2)=((260)(1.26))/(260+(24.0)(2.20)^2)`

`\omega_f=0.87(rad)/(s)=8.31 (rev)/(min)`