Question

To throw the discus, the thrower holds it with a fully outstretched arm. Starting from rest, he begins to turn with a constant angular acceleration, releasing the discus after making one complete revolution. The diameter of the circle in which the discus moves is about 1.6 mm.

If the thrower takes 1.0 s to complete one revolution, starting from rest, what will be the speed of the discus at release?

Answer 1

Step-by-step explanation:

Time taken to complete one revolution is called time period.

So, Time period, T = 1 s

Diameter = 1.6 mm

radius, r = 0.8 mm

Let the angular speed is ω.

The relation between angular velocity and the time period is

`\omega =(2\pi)/(T)`

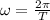
ω = 2 x 3.14 = 6.28 rad/s

The relation between the linear velocity and the angular velocity is

v = r x ω

v = 0.8 x 10^-3 x 6.28

v = 0.005 m/s