Question

Below are three different hypothesis tests about population proportions. For each test, use StatKey and the information given to calculate the appropriate p-value and make the correct conclusion.

(1) H0: p = 0.3 vs Ha: p ? 0.3. In their survey, they had a count of 38 using a sample size n=100.

1.a) What is p-hat for this sample?
Using StatKey, generate a randomization distribution using at least 4000 samples. Remember to select Edit Data to input sample information, and to edit the null hypothesis.
1.b) What is the p-value using this randomization distribution?
1.c) At a significance level of 0.05, what is the conclusion for this hypothesis test?

(2) H0: p = 0.7 vs Ha: p ? 0.7. In their survey, they had a count of 320 using a sample size n=500.

2.a) What is p-hat for this sample?
Using StatKey, generate a randomization distribution using at least 4000 samples. Remember to select Edit Data to input sample information, and to edit the null hypothesis.
2.b) What is the p-value using this randomization distribution?
2.c) At a significance level of 0.05, what is the conclusion for this hypothesis test?

(3) H0: p = 0.6 vs Ha: p < 0.6. In their survey, they had a count of 110 using a sample size n=200.

3.a) What is p-hat for this sample?
Using StatKey, generate a randomization distribution using at least 4000 samples. Remember to select Edit Data to input sample information, and to edit the null hypothesis.
3.b) What is the p-value using this randomization distribution?
3.c) At a significance level of 0.05, what is the conclusion for this hypothesis test?

Answer 1

1a) p-hat=0.38

1b) P=0.08

1c) The null hypothesis is not rejected

2a) p-hat=0.64

2b) P=0.0027

2c) The null hypothesis is rejected

3a) p-hat=0.55

3b) P=0.153

3c) The null hypothesis is not rejected

Explanation:

(1) H0: p = 0.3 vs Ha: p ≠ 0.3. In their survey, they had a count of 38 using a sample size n=100.

1a) The p-hat is p-hat=38/100=0.38.

1b) The standard deviation is

`\sigma=\sqrt{(p(1-p))/(n)}=\sqrt{(0.3*0.7)/(100)}=0.046`

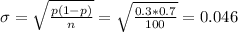
The sample size is n=100.

The z-value is:

`z=\frac{\hat{p}-p}{\sigma}=(0.38-0.3)/(0.046)=(0.08)/(0.046)= 1.74`

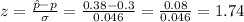
As it is a two-sided test, the p-value considers both tails of the distribution.

The p-value for this |z|=1.74 is P=0.08.

1c) The null hypothesis is not rejected.

(2) H0: p = 0.7 vs Ha: p ≠ 0.7. In their survey, they had a count of 320 using a sample size n=500.

2a) The p-hat is p-hat=320/500=0.64.

2b) The standard deviation is

`\sigma=\sqrt{(p(1-p))/(n)}=\sqrt{(0.7*0.3)/(500)}=0.02`

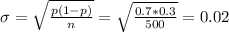
The sample size is n=500.

The z-value is:

`z=\frac{\hat{p}-p}{\sigma}=(0.64-0.7)/(0.02)=(-0.06)/(0.02)=-3`

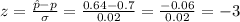
As it is a two-sided test, the p-value considers both tails of the distribution.

The p-value for this |z|=3 is P=0.0027.

2c) The null hypothesis is rejected.

(3) H0: p = 0.6 vs Ha: p < 0.6. In their survey, they had a count of 110 using a sample size n=200.

2a) The p-hat is p-hat=110/200=0.55.

2b) The standard deviation is

`\sigma=\sqrt{(p(1-p))/(n)}=\sqrt{(0.6*0.4)/(200)}=0.035`

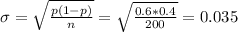
The sample size is n=200.

The z-value is:

`z=\frac{\hat{p}-p}{\sigma}=(0.55-0.6)/(0.035)=(-0.05)/(0.035)=-1.43`

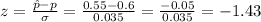
As it is a two-sided test, the p-value considers both tails of the distribution.

The p-value for this |z|=1.43 is P=0.153.

2c) The null hypothesis is not rejected.