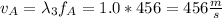Answer:
On wire A the speed is 684 m/s
On wire B the speed is 456 m/s
Step-by-step explanation:
The velocity of a wave is defined as wavelength times frequency of the wave:
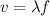 (1)
(1)
with λ the wavelength and f the frequency of the wave.
When you have a wire stretched between two fixed supports, you're going to have standing waves if you perturbate the wire, and the wavelength of the different harmonics you can have is:
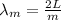
with L the length of the wire and m the number of the harmonic, so for the second harmonic:
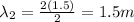
ad for the third harmonic:
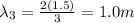
Using those values of wavelength on (1):
For second harmonic:
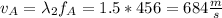
For third harmonic: