Question

A toy manufacturer wants to know how many new toys children buy each year. A sample of 1417 children was taken to study their purchasing habits. Construct the 99% confidence interval for the mean number of toys purchased each year if the sample mean was found to be 7.7. Assume that the population standard deviation is 1.8. Round your answers to one decimal place.

Answer 1

99% confidence interval for the mean number of toys purchased each year is [7.6 , 7.8].

Explanation:

We are given that a toy manufacturer wants to know how many new toys children buy each year. A sample of 1417 children was taken to study their purchasing habits.

Also, the population standard deviation is 1.8.

So, the pivotal quantity for 99% confidence interval for the average age is given by;

P.Q. =
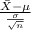`(\bar X - \mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample mean = 7.7

`\sigma` = population standard deviation = 1.8

n = sample of children = 1417

`\mu` = population mean

So, 99% confidence interval for the population mean,
`\mu` is ;

P(-2.5758 < N(0,1) < 2.5758) = 0.99

P(-2.5758 <
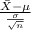`(\bar X - \mu)/((\sigma)/(√(n) ) )` < 2.5758) = 0.99

P(
`-2.5758 * {(\sigma)/(√(n) ) }` <
`{\bar X - \mu}` <
`2.5758 * {(\sigma)/(√(n) ) }` ) = 0.99

P(
`\bar X -2.5758 * {(\sigma)/(√(n) ) }` <
`\mu` <
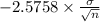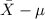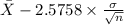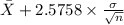`\bar X +2.5758 * {(\sigma)/(√(n) ) }` ) = 0.99

99% confidence interval for
`\mu` = [
`\bar X -2.5758 * {(\sigma)/(√(n) ) }` ,
`\bar X +2.5758 * {(\sigma)/(√(n) ) }` ]

= [
`7.7 -2.5758 * {(1.8)/(√(1417) ) }` ,
`7.7 +2.5758 * {(1.8)/(√(1417) ) }` ]

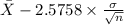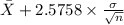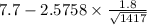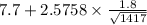= [7.6 , 7.8]

Therefore, 99% confidence interval for the mean number of toys purchased each year is [7.6 , 7.8].

Answer 2

The 99% confidence interval for the mean number of toys purchased each year is between 7.6 toys and 7.8 toys.

Explanation:

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1-0.99)/(2) = 0.005`

Now, we have to find z in the Ztable as such z has a pvalue of
`1-\alpha`.

So it is z with a pvalue of
`1-0.005 = 0.995`, so
`z = 2.575`

Now, find M as such

`M = z*(\sigma)/(√(n))`

In which
`\sigma` is the standard deviation of the population and n is the size of the sample.

`M = 2.575*(1.8)/(√(7.7)) = 0.1`

The lower end of the interval is the sample mean subtracted by M. So it is 7.7 - 0.1 = 7.6 toys

The upper end of the interval is the sample mean added to M. So it is 7.7 + 0.1 = 7.8 toys

The 99% confidence interval for the mean number of toys purchased each year is between 7.6 toys and 7.8 toys.