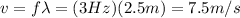Question

The following standing wave below is a 5 m string that vibrates up and down as the four harmonic (4 bumps). The string vibrates 48 cycles in 16 seconds. Determine the string’s speed

Answer 1

7.5 m/s

Step-by-step explanation:

Standing waves are waves that do not propagate, so they are just oscillations of the medium over fixed positions.

Standing waves are produced for example in a string, which is tied at its ends.

The wavelength of the fundamental mode of vibration of a string is equal to twice the length of the string:

`\lambda=2L`

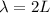
where L is the length of the string.

Here, the string vibrates in its fourth harmonic - this means that the wavelength is actually 1/4 of the wavelength of the fundamental mode:

`\lambda_4=(\lambda)/(4)`

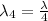
Here, the length of the string is

L = 5 m

So the wavelength of the 4th harmonic is:

`\lambda_4=(\lambda)/(4)=(2L)/(4)=(2(5))/(4)=2.5 m`

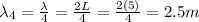
The frequency of the wave is equal instead to the ratio between the number of cycles and the time taken:

`f=(N)/(t)`

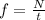
where here

N = 48

t = 16 s

Substituting,

`f=(48)/(16)=3 Hz`

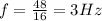
Now we can find the string's speed by using the wave equation; we find:

`v=f\lambda=(3 Hz)(2.5 m)=7.5 m/s`