Question

At a certain temperature, this reaction establishes an equilibrium with the given equilibrium constant, Kc. 3 A ( g ) + 2 B ( g ) − ⇀ ↽ − 4 C ( g ) K c = 2.13 × 10 17 If, at this temperature, 1.80 mol of A and 3.90 mol of B are placed in a 1.00 L container, what are the concentrations of A, B, and C at equilibrium?

Answer 1

The concentrations of A, B, and C at equilibrium:

[A] = 0.0 M

[B] = 2.7 M

[C] = 2.4 M

Step-by-step explanation:

Concentration of 1.80 mol of A in 1.00 L container :

`[A]=(1.80 mol)/(1.00 L)=1.80 M`

Concentration of 3.90 mol of B in 1.00 L container :

`[B]=(3.90 mol)/(1.00 L)=3.90 M`

`3A(g)+2B(g)\rightleftharpoons 4C(g), K_c=2.13* 10^(17)`

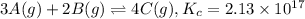
Initially

1.80 M 3.90 M 0

At equilibrium

(1.80-3x)M (3.90-2x) 4x

The expression of an equilibrium constant is given by :

`K_c=([C]^4)/([A]^3[B]^2)`

`2.13* 10^(17)=((4x)^4)/((1.80-3x)^3* (3.90-2x)^2)`

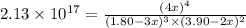
Solving for x:

x = 0.600

The concentrations of A, B, and C at equilibrium:

[A] = [1.80-3x]=[1.80-3 × 0.600]= 0 M

[B] = [3.90-2x] = [3.90-2 × 0.600] = 2.7 M

[C] = [4x] =[4 × 0.600 M] = 2.4 M