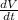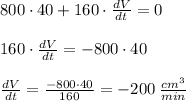Question

Boyle's Law states that when a sample of gas is compressed at a constant temperature, the pressure P and volume V satisfy the equation P V = C , where C is a constant. Suppose that at a certain instant the volume is 800 cm 3 , the pressure is 160 kPa , and the pressure is increasing at a rate of 40 kPa/min . At what rate is the volume decreasing at this instant?

Answer 1

The volume decreasing at the rate of
`200\:(cm^3)/(min)`.

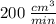Explanation:

We need to find at what rate is the volume decreasing
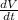`(dV)/(dt)`, when
`V=800\:cm^3`,
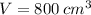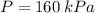`P=160\:kPa`, and
`(dP)/(dt) =40 \:(kPa)/(min)`.

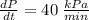We know that when a sample of gas is compressed at a constant temperature, the pressure P and volume V satisfy the equation
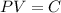`P V = C`, where C is a constant.

So, we can differentiate this equation with respect the time. For this we use the Chain Rule

`\frac{d}{{dx}}\left[ {f\left( u \right)} \right] = \frac{d}{{du}}\left[ {f\left( u \right)} \right]\frac{{du}}{{dx}}`

and the Product rule

`\frac{d}{{dx}}\left( {f\left( x \right)g\left( x \right)} \right) = f\left( x \right)\frac{d}{{dx}}g\left( x \right) + \frac{d}{{dx}}f\left( x \right)g\left( x \right)`

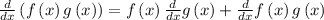
to differentiate both sides with respect to time.

`V(dP)/(dt) +P(dV)/(dt) =(d)/(dt) C\\\\V(dP)/(dt) +P(dV)/(dt) =0`

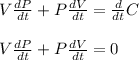
Next, we substitute the given values

`800\cdot 40+160\cdot(dV)/(dt) =0`

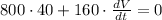
and we solve for
`(dV)/(dt)`

`800\cdot 40+160\cdot(dV)/(dt) =0\\\\160\cdot(dV)/(dt) =-800\cdot 40\\\\(dV)/(dt) =(-800\cdot 40)/(160) =-200\:(cm^3)/(min)`