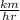Question

A boat is heading due north across a river with a speed of 12.0 km/h relative to the water. The water in the river has a uniform velocity of 6.00 km/h due east relative to the ground. Determine the velocity of the boat relative to an observer standing on either bank.

Answer 1

The velocity of the boat relative to an observer standing on either bank = u = 18
`(km)/(hr)`

Step-by-step explanation:

Let speed of the boat in still water = u
`(km)/(hr)`

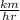
speed of the river water = v
`(km)/(hr)`

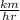
Relative speed of the boat in the water against the river flow is given by

Upstream speed = u - v ------- (1)

⇒ u - v = 12
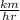`(km)/(hr)` ------ (2)

Given that speed of the water = 6
`(km)/(hr)`

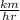
Now velocity of the boat is given From equation (2)

⇒ u = 12 + v

Put the value of v = 6 , we get

⇒ u = 12 + 6

⇒ u = 18
`(km)/(hr)`

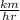
therefore , the velocity of the boat relative to an observer standing on either bank = u = 18
`(km)/(hr)`