Question

`\left \{ {{x+y=1} \atop {x-2y=4}} \right. \\\left \{ {{4x-y=6} \atop {x-y=0}} \right. \\\left \{ {{-x+2y=0} \atop {x+2y=5}} \right. \\\left \{ {{6x-y=-5} \atop {4x-2y=6}} \right.`

These questions need to be solved using Cramer's Rule, If you could please show the work as well, if that's possible, I'd appreciate it!

Answer 1

(a) x=2, y=-1

(b) x=2, y=2

(c)
`\displaystyle x=(5)/(2), y=(5)/(4)`

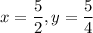
(d) x=-2, y=-7

Explanation:

Cramer's Rule

It's a predetermined sequence of steps to solve a system of equations. It's a preferred technique to be implemented in automatic digital solutions because it's easy to structure and generalize.

It uses the concept of determinants, as explained below. Suppose we have a 2x2 system of equations like:

`\displaystyle \left \{ {{ax+by=p} \atop {cx+dy=q}} \right.`

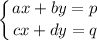
We call the determinant of the system

`\Delta=\begin{vmatrix}a &b \\c &d \end{vmatrix}`

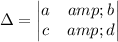
We also define:

`\Delta_x=\begin{vmatrix}p &b \\q &d \end{vmatrix}`

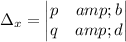
And

`\Delta_y=\begin{vmatrix}a &p \\c &q \end{vmatrix}`

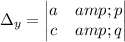
The solution for x and y is

`\displaystyle x=(\Delta_x)/(\Delta)`

`\displaystyle y=(\Delta_y)/(\Delta)`

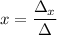
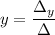
(a) The system to solve is

`\displaystyle \left \{ {{x+y=1} \atop {x-2y=4}} \right.`

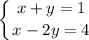
Calculating:

`\Delta=\begin{vmatrix}1 &1 \\1 &-2 \end{vmatrix}=-2-1=-3`

`\Delta_x=\begin{vmatrix}1 &1 \\4 &-2 \end{vmatrix}=-2-4=-6`

`\Delta_y=\begin{vmatrix}1 &1 \\1 &4 \end{vmatrix}=4-3=3`

`\displaystyle x=(\Delta_x)/(\Delta)=(-6)/(-3)=2`

`\displaystyle y=(\Delta_y)/(\Delta)=(3)/(-3)=-1`

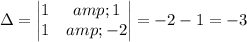
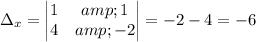
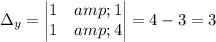
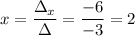
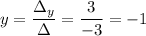
The solution is x=2, y=-1

(b) The system to solve is

`\displaystyle \left \{ {{4x-y=6} \atop {x-y=0}} \right.`

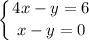
Calculating:

`\Delta=\begin{vmatrix}4 &-1 \\1 &-1 \end{vmatrix}=-4+1=-3`

`\Delta_x=\begin{vmatrix}6 &-1 \\0 &-1 \end{vmatrix}=-6-0=-6`

`\Delta_y=\begin{vmatrix}4 &6 \\1 &0 \end{vmatrix}=0-6=-6`

`\displaystyle x=(\Delta_x)/(\Delta)=(-6)/(-3)=2`

`\displaystyle y=(\Delta_y)/(\Delta)=(-6)/(-3)=2`

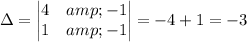
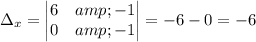
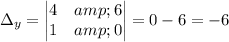
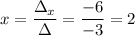
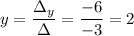
The solution is x=2, y=2

(c) The system to solve is

`\displaystyle \left \{ {{-x+2y=0} \atop {x+2y=5}} \right.`

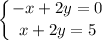
Calculating:

`\Delta=\begin{vmatrix}-1 &2 \\1 &2 \end{vmatrix}=-2-2=-4`

`\Delta_x=\begin{vmatrix}0 &2 \\5 &2 \end{vmatrix}=0-10=-10`

`\Delta_y=\begin{vmatrix}-1 &0 \\1 &5 \end{vmatrix}=-5-0=-5`

`\displaystyle x=(\Delta_x)/(\Delta)=(-10)/(-4)=(5)/(2)`

`\displaystyle y=(\Delta_y)/(\Delta)=(-5)/(-4)=(5)/(4)`

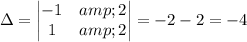
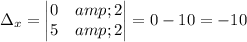
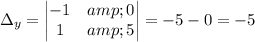
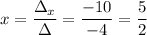
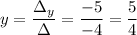
The solution is

`\displaystyle x=(5)/(2), y=(5)/(4)`

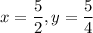
(d) The system to solve is

`\displaystyle \left \{ {{6x-y=-5} \atop {4x-2y=6}} \right.`

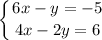
Calculating:

`\Delta=\begin{vmatrix}6 &-1 \\4 &-2 \end{vmatrix}=-12+4=-8`

`\Delta_x=\begin{vmatrix}-5 &-1 \\6 &-2 \end{vmatrix}=10+6=16`

`\Delta_y=\begin{vmatrix}6 &-5 \\4 &6 \end{vmatrix}=36+20=56`

`\displaystyle x=(\Delta_x)/(\Delta)=(16)/(-8)=-2`

`\displaystyle y=(\Delta_y)/(\Delta)=(56)/(-8)=-7`

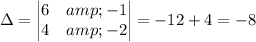
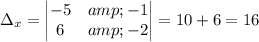
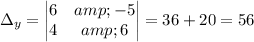
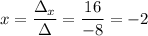
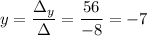
The solution is x=-2, y=-7