Answer:
The distance of the google to the edge of the pool is 4.75 mm
Step-by-step explanation:
The angle made by the laser and surface of the pool denoted as β, is calculated as follows;
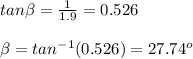
The incident of the laser beam = 90 - 27.74 = 62.26°
Apply Sneil's law to calculate refracted angle of air-water interface
Refractive index of air, na = 1
Refractive index of water, nw = 1.33
na(sinθi) = nw(sinθr)
where;
θi is the incident of the laser beam
θr is refracted angle of the laser beam in water
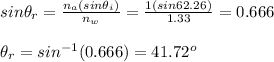
The displacement of the refracted laser beam, d is calculated as follows;
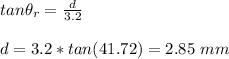
The distance of the google to the edge of the pool = 1.9 mm + 2.85 mm
= 4.75 mm
Check the image uploaded for the diagram and for better understanding.