The positive value for x is 7
Step-by-step explanation:
Given that the area of a rectangle is expressed by
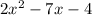
The area of the rectangle is 45.
We need to determine the positive value for x.
The value for x:
The value of x can be determined by equating both the values of area of a rectangle.
Thus, we have,
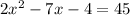
Subtracting both sides by 45, we have;

Let us solve the equation using the quadratic formula.
Thus, we get;
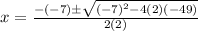
Simplifying, we get;
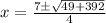

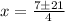
Thus, the two values of x are given by
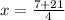 and
and
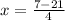
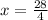 and
and
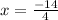
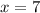 and
and
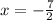
Since, x cannot take negative values, then
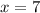
Thus, the value of x is 7.