Question

12. A bank manager estimates that an average of two customers enters the tellers' queue every five minutes. Assume that the number of customers that enters the tellers' queue is Poisson distributed. What is the probability that exactly seven customers enter the queue in a randomly selected 15-minute period

Answer 1

13.77% probability that exactly seven customers enter the queue in a randomly selected 15-minute period

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

A bank manager estimates that an average of two customers enters the tellers' queue every five minutes.

We are working in a fifteen minutes interval, so
`\mu = (15*2)/(5) = 6`

What is the probability that exactly seven customers enter the queue in a randomly selected 15-minute period

This is P(X = 7).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 7) = (e^(-6)*(6)^(7))/((7)!) = 0.1377`

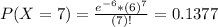
13.77% probability that exactly seven customers enter the queue in a randomly selected 15-minute period