Question

18. Triangle JKL is located at J(-8,-3)

K(-8,-6) and L(-5, -6). A transformation
occurred and now the triangle is located
at J(8,-3) K (8,-6) and L(5,-6). What
transformation occurred?

Answer 1

Given that the triangle JKL is located at J(-8,-3) , K(-8,-6) and L(-5, -6).

A transformation occurred and the triangle is located at J(8,-3) K (8,-6) and L(5,-6).

We need to determine the type of transformation.

Let us consider the transformation for the point J
`(-8,-3) \rightarrow (8,-3)`

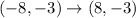
Thus, the transformation rule for the point J is
`(x,y)\rightarrow (-x,y)`

Hence, the point is reflected across y - axis.

Considering the transformation for the point K
`(-8,-6) \rightarrow (8,-6)`

Thus, the transformation rule for the point K is
`(x,y)\rightarrow (-x,y)`

Hence, the point is reflected across y - axis.

Finally, considering the transformation for the point L
`(-5,-6) \rightarrow (5,-6)`

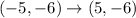
Thus, the transformation rule for the point L is
`(x,y)\rightarrow (-x,y)`

Hence, the point is reflected across y - axis.

Therefore, the triangle JKL is reflected across y - axis.

The transformation occurred is
`(x,y)\rightarrow (-x,y)`