Answer:
Explanation:
Hello!
The objective is to compare the average tread life of two brands of radial tires. Two random samples of 15 tires each was taken and the distance (in thousands of miles) the tread lasted was recorded.
a. Boxplots in 2nd attachment.
As you can see both variables boxes are the same size, both of them show the equal distance between the quantiles which is compatible with a symmetrical distribution. Me sample mean (black square) is in the center of the boxes and the whiskers are also equidistant. Looking at the graphics you can assume that both study variables have a normal distribution.
b.
X₁: Distance the tire tread of a brand 1 radial tire lasts.
n₁= 15
X[bar]₁= 52
S₁= 4.61
X₂: Distance the tire tread of a brand 2 radial tire lasts.
n₂= 15
X[bar]₂= 56.93
S₂= 4.83
The objective is to test if there is any difference between the two brands, to do so you have to compare the average distance the tread lasts:
H₀: μ₁ = μ₂
H₁: μ₁ ≠ μ₂
α: 0.01
The statistic to use for this test is a student t for indepeendent samples with pooled standard deviation:
![t= \frac{(X[bar]_1-X[bar]_2)(Mu_1-Mu_2)}{Sa\sqrt{(1)/(n_1) +(1)/(n_2) } } ~~t_(n_1+n_2-2)](https://img.qammunity.org/2021/formulas/mathematics/college/e9xoadv7zacju44exjb9lrtzf8mp90np9q.png)
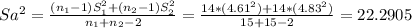
Sa= 4.72
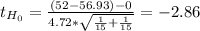
The p-value for this test is two-tailed and you can calculate it doing the following calculations:
P(t₂₈≤-2.86) + P(t₂₈≥2.86)= P(t₂₈≤-2.86) + 1 - P(t₂₈≤2.86)= 0.0040 + (1 - 0.9960)= 0.008
p-value: 0.008
Since the p-value is less than the significance level, the decision is to reject the null hypothesis. at a 1% significance level, you can conclude that the expected of the tread life of radial tires of brand 1 is different than the expected tread life of radial tires of brand 2.
c.
You have to create a 99% CI for the difference between the population means of tread life of tires from brand 1 and 2, the formula for the CI is:
(X[bar]₁-X[bar]₂)±
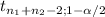 *(Sa*√(1/n₁+1/n₂))
*(Sa*√(1/n₁+1/n₂))
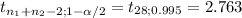
(52-56.93)±2.763*(4.72*√1/15+1/15)
[-9.69;-0.17]
With a 99% confidence level, you'd expect that the interval [-9.69;-0.17] will contain the difference between the expected tread life of the radial tires of brand 1 and the expected tread life of the radial tires of brand 2.
I hope you have a SUPER day!