Question

Write the slope-intercept form of the equation of the line described below.

Through- (-5,-3) , Slope = -2/5

Answer 1

The equation of the line is
`y=-(2)/(5)x-5`

Step-by-step explanation:

Given that the line passes through the points (-5,-3)

The slope of the line is
`m=-(2)/(5)`

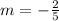
We need to determine the equation of the line.

Equation of the line:

The equation of the line can be determined using the formula,

`y-y_1=m(x-x_1)`

Let us substitute the points (-5,-3) and the slope
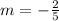`m=-(2)/(5)` in the above formula.

Thus, we have;

`y+3=-(2)/(5)(x+5)`

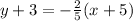
Simplifying, we get;

`y+3=-(2)/(5)x-2`

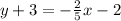
Subtracting 3 from both sides of the equation, we get;

`y=-(2)/(5)x-5`

Hence, the equation of the line in slope - intercept form is
`y=-(2)/(5)x-5`