Question

Jason hired a luxury car service. The service charges a fixed rate of $10.95, regardless of the number of miles traveled, plus an additional $3.71 per mile. If Jason wants to spend no more than $4.44 per mile, what is the minimum number of miles he should travel?

Answer 1

The minimum number of miles he should travel is 15 miles

Explanation:

Let

x ---> the number of miles traveled

we know that

The number of miles traveled multiplied by $3.71 per mile plus a fixed rate of $10.95 must be less than or equal to the number of miles multiplied by $4.44 per mile

so

The inequality that represent this situation is

`10.95+3.71x\leq 4.44x`

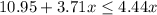
solve for x

subtract 3.71x both sides

`10.95\leq 4.44x-3.71x`

`10.95\leq 0.73x`

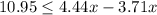
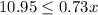
Divide by 0.73 both sides

`15\leq x`

Rewrite

`x\geq 15`

therefore

The minimum number of miles he should travel is 15 miles