Answer:
The function
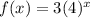 forms a geometric sequence ⇒ 1st answer
forms a geometric sequence ⇒ 1st answer
Explanation:
In the geometric sequence there is a common ratio between each two consecutive terms
Lets substitute x by 1, 2, 3 to find the first three terms and check if there is a common ratio between the consecutive terms or not
∵
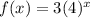
∵ x = 1, 2 , 3
- Substitute x by 1
∴
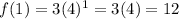
- Substitute x by 2
∴

- Substitute x by 3
∴
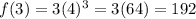
∴ The sequence is 12, 48, 192, .......
- Let us check the ratio between each two consecutive terms
∵ 48 ÷ 12 = 4
∵ 192 ÷ 48 = 4
- There is a constant ratio 4 between the consecutive terms
∴ The function
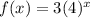 forms a geometric sequence
forms a geometric sequence
∵ f(x) = 3(x)²
∵ x = 1, 2 , 3
- Substitute x by 1
∴ f(1) = 3(1)² = 3(1) = 3
- Substitute x by 2
∴ f(2) = 3(2)² = 3(4) = 12
- Substitute x by 3
∴ f(3) = 3(3)² = 3(9) = 27
∴ The sequence is 3, 12, 27, .......
- Let us check the ratio between each two consecutive terms
∵ 12 ÷ 3 = 4
∵ 27 ÷ 12 = 2.25
- There is no constant ratio 4 between the consecutive terms
∴ The function f(x) = 3(x)² does not form a geometric sequence
∵ f(x) = 2x + 4
∵ x = 1, 2, 3
- Substitute x by 1
∴ f(1) = 2(1) + 4 = 2 + 4 = 6
- Substitute x by 2
∴ f(2) = 2(2) + 4 = 4 + 4 = 8
- Substitute x by 3
∴ f(3) = 2(3) + 4 = 6 + 4 = 10
∴ The sequence is 6, 8, 10, .......
- Let us check the ratio between each two consecutive terms
∵ 8 ÷ 6 =

∵ 10 ÷ 8 =

- There is no constant ratio 4 between the consecutive terms
∴ The function f(x) = 2x + 4 does not form a geometric sequence
∵ f(x) = x +
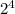
∵ x = 1, 2, 3
- Substitute x by 1
∴ f(1) = 1 +
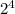 = 1 + 16 = 17
= 1 + 16 = 17
- Substitute x by 2
∴ f(2) = 2 +
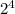 = 2 + 16 = 18
= 2 + 16 = 18
- Substitute x by 3
∴ f(3) = 3 +
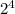 = 3 + 16 = 19
= 3 + 16 = 19
∴ The sequence is 17, 18, 19, .......
- There is a common difference 1 (not a common ratio) between
the consecutive terms
∴ The function f(x) = x +
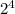 does not form a geometric sequence
does not form a geometric sequence