Answer:
The maximum length of specimen is 0.475 m
Step-by-step explanation:
Given :
Maximum elongation
 m
m
Tensile force
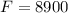 N
N
Diameter
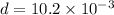 m
m
Elastic modulus
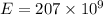 Pa
Pa
So area of cylindrical specimen is given by,

From the formula of elongation,
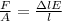
Where
 maximum length of specimen,
maximum length of specimen,
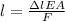
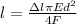
Put the value and find maximum length,

 m
m