Question

Suppose a bowler claims that her bowling score is less than 116 points, on average. Several of her teammates do not believe her, so the bowler decides to do a hypothesis test, at a 5% significance level, to persuade them. She bowls 25 games. The mean score of the sample games is 103 points. The bowler knows from experience that the standard deviation for her bowling score is 19 points.

H0: μ≥116; Ha: μ<116
α=0.05 (significance level)

What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places?

Answer 1

Test statistic (z-score) of this one-mean hypothesis test is -3.42.

Explanation:

We are given that a bowler claims that her bowling score is less than 116 points, on average. She bowls 25 games. The mean score of the sample games is 103 points. The bowler knows from experience that the standard deviation for her bowling score is 19 points.

We have to test if the bowler claim is correct or not.

Let Null Hypothesis,
`H_0` :
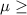`\mu \geq` 116 {means that the bowler claim is correct}

Alternate Hypothesis,
`H_1` :
`\mu` < 116 {means that the bowler claim is not correct}

The test statistics that will be used here is One-sample z-test statistics;

T.S. =
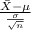`(\bar X - \mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample mean score = 103 points

`\sigma` = population standard deviation = 19 points

n = sample of games = 25

So, test statistics =
`(103-116)/((19)/(√(25) ) )`

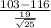
= -3.42

Therefore, the test statistic (z-score) of this one-mean hypothesis test is -3.42.