Question

Find the distance between (2a+2, 2b) and (2b+2, 2a), given that a>b.

Answer 1

Distance =
`2√(2)a-2√(2)b`

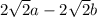
Explanation:

We will use distance formula shown below to solve this:

Distance Formula:
`√((y_2-y_1)^2+(x_2-x_1)^2)`

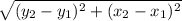
Where

x_1 = 2a + 2

y_1 = 2b

x_2 = 2b+2

y_2 = 2a

Substituting, we solve for the expression for distance:

`D=√((y_2-y_1)^2+(x_2-x_1)^2)\\D=√((2a-2b)^2+((2b+2)-(2a+2))^2)\\D=√((2a-2b)^2+(2b+2-2a-2)^2)\\D=√((2a-2b)^2+(2b-2a)^2)\\D=√(4a^2 -8ab+4b^2+4b^2-8ab+4a^2)\\D=√(8a^2-16ab+8b^2)\\D=\sqrt{(2√(2)a-2√(2)b)^2}\\D=2√(2)a-2√(2)b`

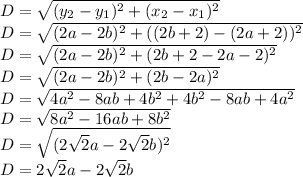
This is the expression in terms of a, and b, given a > b