Question

MISU CR Geomeuy B

English
Jauull
An acute triangle has side lengths 21 cm, x cm, and 2x cm. If 21 is one of the shorter sides of the triangle, what is the
greatest possible length of the longest side, rounded to the nearest tenth?
18.8 cm
24.2 cm
42.0 cm
72.7 cm

Answer 1

42 cm is the greatest possible length of the longest side . Correct option C)42 cm

Explanation:

We have , An acute triangle has side lengths 21 cm, x cm, and 2x cm. If 21 is one of the shorter sides of the triangle, We need to find what is the greatest possible length of the longest side, rounded to the nearest tenth . Let's find out:

The Triangle Inequality Theorem states that the sum of any two sides of a triangle must be greater than the measure of the third side so:

case a)
`21+x>2x`

⇒
`21+x-x>2x-x`

⇒
`21>x`

⇒
`x<21cm`

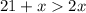
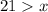
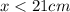
case b)
`x+2x<21`

⇒
`3x<21`

⇒
`x<7cm`

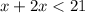
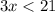
Therefore , the longest side is 2x i.e.

`x<21cm\\2x<42cm`

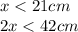
the longest side could be 41.99 cm rounded to the nearest tenth is 42 cm

Therefore , 42 cm is the greatest possible length of the longest side . Correct option C)42 cm