Question

A distribution of a large sample of weights follows a normal distribution with mean 80.4 kilograms. If approximately 68% of the weights are between 78.1 kilograms and 82.7 kilograms, what is the standard deviation of this distribution?

Answer 1

The standard deviation of this distribution is 2.3 kilograms.

Explanation:

The Empirical Rule states that, for a normally distributed random variable:

68% of the measures are within 1 standard deviation of the mean.

95% of the measures are within 2 standard deviation of the mean.

99.7% of the measures are within 3 standard deviations of the mean.

In this problem, we have that:

Approximately 68% of the weights are between 78.1 kilograms and 82.7 kilograms.

This means that 78.1 is one standard deviation below the mean and 82.7 is one standard deviation above the mean.

Using one of them

`82.7 = 80.4 + \sigma`

`\sigma = 82.7 - 80.4`

`\sigma = 2.3`

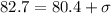
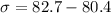
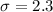
The standard deviation of this distribution is 2.3 kilograms.