Question

If Martin deposited \$2,11 into an account and earned $750 of interest over 5 years, how much was the interest rate?

Answer 1

The interest rate is 7.1%

Explanation:

It is given that,

• The amount Martin deposited into the account, P = $2,110
• The interest he earned, I = $750
• The time period, t = 5 years.

To find the interest rate :

The formula used here is given by,

Interest = P× r× t

where,

• P is the principal amount deposited in the account.
• t is the time period
• r is the interest rate

Now, substituting P= $211 , t= 5 and I = $750

⇒ 750 = 2110 × 5 × r

⇒ 750 = (10550×r)

⇒ 750 ÷ 10550 = r

⇒ r = 0.071

The rate should be represented in the percentage, therefore, multiply it by 100.

Interest rate = 0.071 × 100

Rate = 7.1 %

∴ The interest rate is 7.1%

Answer 2

5.90% much was the interest rate .

Explanation:

Here we have , If Martin deposited \$211 into an account and earned $750 of interest over 5 years, We need to find how much was the interest rate . Let's find out:

Let us suppose that interest rate was x% per month! So , Amount of money he earned as interest per month :

⇒
`(211(x))/(100)`

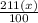
Now , For one year( 12 months ) he earned :

⇒
`(211(x))/(100)(12)`

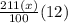
∴For five year he earned :

⇒
`(211(x))/(100)(12)(5)`

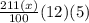
According to question , he earned $750 of interest over 5 years i.e.

⇒
`(211(x))/(100)(12)(5) =750`

⇒
`(211(x))/(100)(60) =750`

⇒
`x =(750(100))/(211(60)`

⇒
`x =5.90\%`

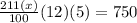
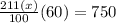
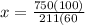
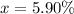
Therefore , 5.90% much was the interest rate .