Answer:
3.6 hours
Explanation:
Alan's revenue function is given by:
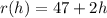
for every h hours he spends repairing televisions.
His overhead cost is modeled by the function:
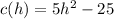
To find the number of hours Alan breaks even, we need to equate the functions and solve for h.

We rewrite in standard form:
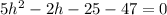
This gives:
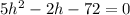
Using the quadratic formula:
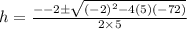
This gives:
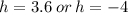
Since time is not negative, he breaks even after 3.6 hours.