Question

The value of a brand new SUV is currently $15,400. After every year, the value of the SUV decreases by 10%.

a)First construct an exponential decay equation:

(A) V = 15400(1 – 10)t

(B) V = 15400(1 – 0.10)t

(C) V = 15400(0.10)t

(D) V = 15400(10 – 0.10)t

b) When will the value of the SUV be $12,465?

t =

(A) 1 year

(B) 2 years

(C) 3 years

(D) 4 years

Answer 1

`a.\ \ \ V=15400(1-0.1)^t`

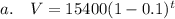
b. 2 yrs

Explanation:

-Given the initial value at time t=0 as $15,400 and the decay rate as 10%.

-The exponential decay is given by the formula;

`y=a(1-r)^x\\\\x-time\\r-decay \ rate\\a-initial \ value\\y-value \ at\ time \ x`

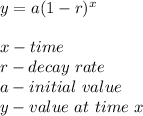
We can therefore write our decay expression as;

`V=a(1-r)^t\\\\=15400(1-0.10)^t`

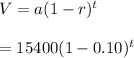
Hence, our exponential decay equation is
`V=15400(1-0.1)^t`

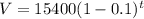
b. Having determined the decay function as
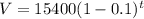`V=15400(1-0.1)^t`, we make $12465 our y value and solve for time, t;

`V=15400(1-0.1)^t\\\\12465=15400(1-0.1)^t\\\\12465=15400(0.9^t)\\\\0.809416=0.9^t\\\\t=(log \ 0.809416)/(log \ 0.9)\\\\=2.0\ yrs`

Hence, the value of the car will be $12,465 after 2 years