Question

A fuse in an electric circuit is a wire that is designed to melt, and thereby open the circuit, if the current exceeds a predetermined value. Suppose that the material to be used in a fuse melts when the current density rises to 520 A/cm2. What diameter of cylindrical wire should be used to make a fuse that will limit the current to 0.62 A

Answer 1

0.0389 cm

Step-by-step explanation:

The current density in a conductive wire is given by

`J=(I)/(A)`

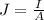
where

I is the current

A is the cross-sectional area of the wire

In this problem, we know that:

- The fuse melts when the current density reaches a value of

`J=520 A/cm^2`

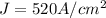
- The maximum limit of the current in the wire must be

I = 0.62 A

Therefore, we can find the cross-sectional area that the wire should have:

`A=(I)/(J)=(0.62)/(520)=1.19\cdot 10^(-3) cm^2`

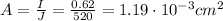
We know that the cross-sectional area can be written as

`A=\pi (d^2)/(4)`

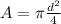
where d is the diameter of the wire.

Re-arranging the equation, we find the diameter of the wire:

`d=\sqrt{(4A)/(\pi)}=\sqrt{(4(1.19\cdot 10^(-3)))/(\pi)}=0.0389 cm`