Answer:

Explanation:
Assuming the situation can be modelled using a linear equation, then the line must pass through the point (2,54) and (4,100).
To find the equation of this line, we determine the slope using:
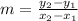
Substitute the coordinates of the points:
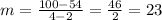
We use the following formula to find the equation of this line.

We substitute the first point a d slope to get:
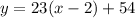
Expand the parenthesis to get:
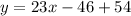
This simplifies to

This is the slope-intercept from.