Question

Use the remainder theorem to find the remainder of 2x^4 + x^2 - 10x -1 divided by x +2.

Answer 1

The remainder is 55

Explanation:

Let

`p(x)= 2 {x}^(4) + {x}^(2) - 10x - 1`

According to the remainder theorem, if p(x) is divided by x+a, the remainder is p (-a).

The given divisor is x+2, therefore the remainder is given by:

`p( - 2)`

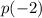
We substitute x=-2 to get:

`p( - 2)= 2 {( - 2)}^(4) + {( - 2)}^(2) - 10( - 2) - 1`

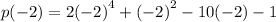
We simplify to obtain:

`p( - 2)= 2 * 16 + 4 + 20- 1`

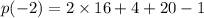
We multiply to get:

`p( - 2)=3 2 + 4 + 20- 1 = 55`

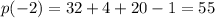
Therefore the remainder is 55