sin θ =
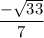
tan θ =
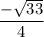
Explanation:
It is given that, cos θ =
 then csc θ < 0, which implies that the θ is in the quadrant IV. Since cos θ is
then csc θ < 0, which implies that the θ is in the quadrant IV. Since cos θ is
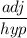 , we need to find the opposite side x.
, we need to find the opposite side x.
Using the Pythogarus theorem, we can find the sin and the tan θ as,
7² = 4² + x²
x² = 7² - 4²
x² = 49 - 16
x² = 33
Taking sqrt on both sides, we will get,
x =

Using the value of x, we can write the sine and tan ratio as,
sin θ =
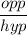 =
=
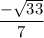
tan θ =
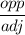 =
=
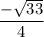
Thus we have obtained the values of sin θ and tan θ