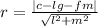Answer:
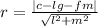
Explanation:
The given circle has equation
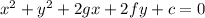
This circle has centre (-g,-f).
For the line
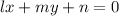
to be a tangent to this circle, the perpendicular distance from the center to this line must be equal to the radius of the circle.
This is given by:

We substitute the center and radius to get:
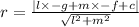
We simplify to get;