Question

Explain why the equation below has two solutions. Then solve the equation to find the solutions. Must show all work and have a written explanation to receive full credit.

(x+3)^2+8=72
Answer:

Answer 1

x = 5, -11

Explanation:

(x+3)² + 8 = 72

(x + 3)² = 64

When you square root both sides, put a +- with root(64)

(x + 3) = 8

x = 5

(x + 3) = -8

x = -11

Answer 2

The solutions are x=-11 and x=5

Explanation:

we have

`(x+3)^2+8=72`

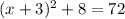
Is a quadratic equation or equation of second degree.

The degree (largest exponent) is 2 so the maximum number of roots (solutions) is 2

Solve for x

`(x+3)^2=72-8`

`(x+3)^2=64`

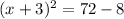
take square root both sides

`x+3=\pm8`

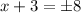
subtract 3 both sides

`x=-3\pm8`

`x=-3+8=5`

`x=-3-8=-11`

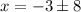
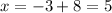
therefore

The solutions are x=-11 and x=5