Question # 1
Answer:
It would cost
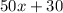 dollars to put fencing around this garden.
dollars to put fencing around this garden.
Explanation:
In Linda's garden each side is:
- either
 feet or
feet or
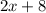 feet
feet
so
We need to determine the perimeter of the rectangle in order to figure out how much fencing there is.

As price per foot of fencing is 5 dollars.
So multiply this by 5 dollars.
![5\left(P\right)=5\left[\left(3x-5\right)+\left(2x+8\right)+\left(3x-5\right)+\left(2x+8\right)\right]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/x6g8w8u1l6xex46yt4awqpkde1bzr6caoj.png)
solving
![5\left[\left(3x-5\right)+\left(2x+8\right)+\left(3x-5\right)+\left(2x+8\right)\right]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/1g1w5qyxba17shmujwp1rabmyr8ojii3xs.png)

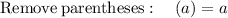
![=5\left(3x-5+2x+8+3x-5+2x+8\right)...[A]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/hux865z5ftsw3gm3tq67guftaykeaxc25d.png)
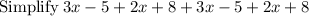
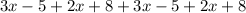
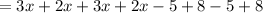
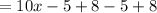
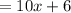
so Equation [A] becomes
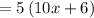
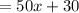
Therefore, it would cost
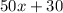 dollars to put fencing around this garden.
dollars to put fencing around this garden.
Question # 2
Answer:
The possible dimensions of the rectangle are
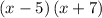 .
.
Explanation:
As the rectangle has the area =
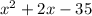
As
Area = Length × Width
The dimensions of the rectangle could be found by factoring the area:
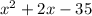
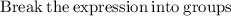


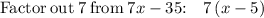
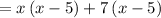
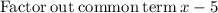

Therefore, the possible dimensions of the rectangle are
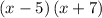 .
.