Question

A consumer products company found that 42​% of successful products also received favorable results from test market​ research, whereas 11​% had unfavorable results but nevertheless were successful. That​ is, P(successful product and favorable test ​market)equals0.42 and​ P(successful product and unfavorable test ​market)equals0.11. They also found that 35​% of unsuccessful products had unfavorable research​ results, whereas 12​% of them had favorable research​ results, that is​ P(unsuccessful product and unfavorable test ​market)equals0.35 and​ P(unsuccessful product and favorable test ​market)equals0.12. Find the probabilities of successful and unsuccessful products given known test market​ results, that​ is, P(successful product given favorable test​ market), P(successful product given unfavorable test​ market), P(unsuccessful product given favorable test​ market), and​ P(unsuccessful product given unfavorable test​ market).

Answer 1

(1) The probability of a successful product given the product is favorable is 0.7778.

(2) The probability of a successful product given the product is unfavorable is 0.2391.

(3) The probability of a unsuccessful product given the product is favorable is 0.2222.

(4) The probability of a unsuccessful product given the product is favorable is 0.7609.

Explanation:

Denote the events as follows:

S = a product is successful.

F = a product is favorable.

The information provided is:

`P(S\cap F)=0.42\\P(S\cap F^(c))=0.11\\P(S^(c)\cap F)=0.12\\P(S^(c)\cap F^(c))=0.35\\`

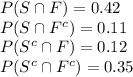
The law of total probability states that:

`P(A)=P(A\cap B)+P(A\cap B^(c))`

Use the law of total probability to compute the probability of a favorable product as follows:

`P(F)=P(S\cap F)+P(S^(c)\cap F)\\=0.42+0.12\\=0.54`

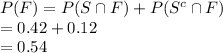
The probability of a favorable product is 0.54.

The conditional probability of an event A given that another event B has already occurred is:

`P(A|B)=(P(A\cap B))/(P(B))`

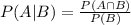
(1)

Compute the value of P (S|F) as follows:

`P(S|F)=(P(S\cap F))/(P(F))=(0.42)/(0.54)=0.7778`

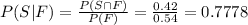
Thus, the probability of a successful product given the product is favorable is 0.7778.

(2)

Compute the value of
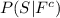`P(S|F^(c))` as follows:

`P(S|F^(c))=(P(S\cap F^(c)))/(P(F^(c)))=(0.11)/((1-0.54))=0.2391`

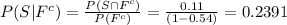
Thus, the probability of a successful product given the product is unfavorable is 0.2391.

(3)

Compute the value of
`P (S^(c)|F)` as follows:

`P (S^(c)|F)=(P(S^(c)\cap F))/(P(F))=(0.12)/(0.54)=0.2222`

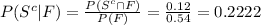
Thus, the probability of a unsuccessful product given the product is favorable is 0.2222.

(4)

Compute the value of
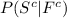`P (S^(c)|F^(c))` as follows:

`P (S^(c)|F)=(P(S^(c)\cap F^(c)))/(P(F^(c)))=(0.35)/((1-0.54))=0.7609`

Thus, the probability of a unsuccessful product given the product is favorable is 0.7609.